MAAGC Poster: K-Theoretic Catalans
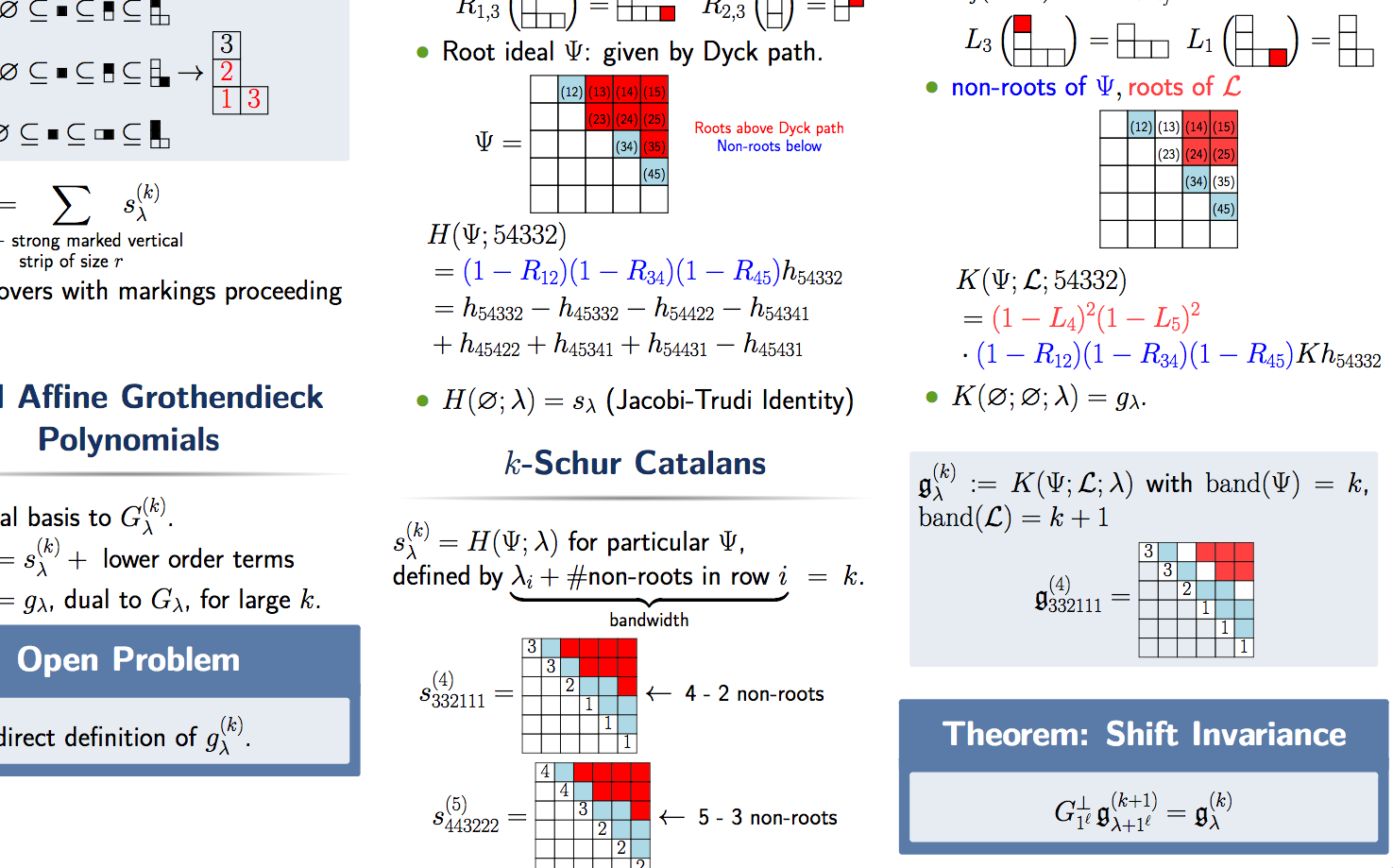
This last weekend, I had an opportunity to attend and present a poster at the 2019 Mid-Atlantic Algebra, Geometry, and Combinatorics (MAAGC) conference in Philadelphia. The poster is about one of the projects I am currently working on to describe “\(K\)-theoretic \(k\)-Schur functions” with a raising operator formula which is a specialization of what we are currently calling “\(K\)-theoretic Catalan functions” since they generalize the description of Catalan functions that Blasiak, Morse, Pun, and Summers used to prove the Schur positivity of \(k\)-Schur functions.
A PDF of my poster is available here, but I also want to provide an overview for those who could not attend in person and listen to my oral summry.
It is well-known that Schur functions give explicit representatives for the Schubert classes in the cohomology of the Grassmannian. It is also known that Grothendieck polynomials play a similar role for the \(K\)-theory classes of the Grassmannian. However, this project concerns the symmetric functions that play a similar role for the affine Grassmannian. The (co)homology representatives in this context are the dual \(k\)-Schur functions and the \(k\)-Schur functions.
Many desired results for these functions are well known. Specifically, they have
- A monomial description as a weight generating function over special tableaux;
- A description of the Pieri rule for the dual \(k\)-Schur functions, which is logically equivalent to a dual Pieri rule;
- A branching rule that gives the \((k+1)\)-Schur expansion of \(k\)-Schur functions.
The \(K\)-theory representatives for the affine Grassmannian have been shown to be affine Grothendieck polynomials and dual affine Grothendieck polynomials (sometimes called \(K\)-\(k\)-Schur functions). Just like with the (co)homology picture, we desire the properties above. However, we have only
- A monomial description as a weight generating function over “affine set-valued tableaux” for the affine Grothendieck polynomials, but no description for the dual affine Grothendieck polynomials;
- No description of the Pieri rule for the affine Grothendieck polynomials;
- Only a conjecture that the coefficients in the \((k+1)\) dual affine Grothendieck expansion of the \((k)\) dual affine Grothendieck polynomials are “positive” (in the \(K\)-theoretic sense).
With this project, we hope to fill in these gaps by using new Catalan function techniques that have successfully solved long standing questions about \(k\)-Schur functions. To this end, we have a (conjectured) raising operator formula for the dual affine Grothendieck polynomials and have shown that they satisfy a key property called shift invariance, which then establishes that the branching coefficients are computable using the dual vertical Pieri rule. Thus, if we can establish the dual vertical Pieri rule for these affine Grothendieck polynomials using the raising operator formula, we will solve the branching problem as a corollary. We have seen some initially promising results towards doing this using Catalan function type techniques, so I am hopeful this work will lead to filling in the missing pieces of this \(K\)-theory picture.
Finally, the poster does not include references, but the primary ones are:
- J. Blasiak, J. Morse, A. Pun, D. Summers, Catalan Functions and \(k\)-Schur Positivity, Journal of the AMS (2019).
- A. S. Buch, Combinatorial \(K\)-theory, Topics in Cohomological Studies of Algebraic Varieties (2005), 87–-104.
- T. Lam and P. Pylyavskyy, Combinatorial Hopf Algebras and \(K\)-Homology of Grassmannians, International Mathematics Research Notices (2007).
- T. Lam, A. Schilling, M. Shimozono, \(K\)-theory Schubert calculus of the affine Grassmannian, Compositio Math. (2010), 811–852.
- J. Morse, Combinatorics of the \(K\)-theory of affine Grassmannians, Advances in Mathematics (2011).
Date published: Friday, May 10, 2019