George H. Seelinger

These notes are when I guest lectured in Thomas Lam’s class on Symmetric Functions in Winter 2024. I modeled my notes off of Mark Haiman’s presentation of Hall-Littlewood polynomials and Macdonald polynomials for his Math 249 class in the Spring 2020 term at UC Berkeley. Contrasting from Macdonald’s book, in these talks I take as a starting point the Schur-positive Hall-Littlewood polynomials and define them in a way that is most easily compatible with the construction of “Catalanimals” from my research with collaborators. Many facts were not proven due to time constraints, but my hope is that these notes provide a nice overview about a good way to think about Hall-Littlewood and Macdonald polynomials.

Extended abstract is available here.

Abstract: The Shuffle Theorem, conjectured by Haglund, Haiman, Loehr, Remmel and Ulyanov, and proved by Carlsson and Mellit, describes the characteristic of the $S_n$-module of diagonal harmonics as a weight generating function over labeled Dyck paths under a line with slope −1. The Shuffle Theorem has been generalized in many different directions, producing a number of theorems and conjectures. We provide a generalized shuffle theorem for paths under any line with negative slope using different methods from previous proofs of the Shuffle Theorem. In particular, our proof relies on showing a “stable” shuffle theorem in the ring of virtual GL_l-characters. Furthermore, we use our techniques to prove the Extended Delta Conjecture, yet another generalization of the original Shuffle Conjecture.

During these unprecedented times, I have seen a number of creative alternatives to in person talks. One of these solutions is the Junior Mathematian Research Archive. Essentially, early career researchers can propose to submit a video about a paper they have recently submitted to arXiv. So, I figured I would give it a shot and gave a short talk about part of my paper with Jonah Blasiak and Jennifer Morse on \(K\)-theoretic Catalan functions.

This past semester (Fall 2019), I taught “flipped calculus” for the first time at UVA. It was a whirlwind experience with many challenging but also rewarding aspects. As one professor told me “I do not want to hear your abstract teaching philosophy” and so I wish to clarify that this write-up is merely a reflection on my experiences and lessons learned while teaching this new classroom model; it is not meant to be didactic.

This past week I had the opportunity to give my first public research presentation as a graduate student at Adriano Garsia’s 90th birthday conference, Garsiafest, in San Diego at the Scripps Seaside Forum. My presentation mainly expanded on the information from my MAAGC Poster, but now one of the main conjectures is a theorem! You can look at the slides here. Eventually, they will also post a video of my talk on the conference website. It was truly an honor to present my work to so many people in my area and I look forward to presenting more work in the future.

This past week, I was lucky enough to meet and attend some lectures given by Ole Warnaar at the Virginia Integrable Probability Summer School 2019 on Schur Functions and Schur Processes since I was not traveling. As someone who does research in symmetric function theory, I had already seen much of what Dr. Warnaar presented in his lecture series (which is all recorded and posted online at the linked course page), but I used the opportunity to make some significant additions to my notes on plethystic substitution. In particular, I had never seen an introductory lecture on plethystic substitution for symmetric functions despite using and seeing it in research papers, and so it was a great opportunity to learn something new at a basic level. Furthermore, his approach was different to what I had seen in Macdonald’s book, so it was great to get a different persepctive on it all. I was also curious to learn more about Schur processes since I do not think about probability for my research at the moment, but unfortunately there was not enough time to get too deep into the subject. I hope I will have a chance to learn more about it later, though!

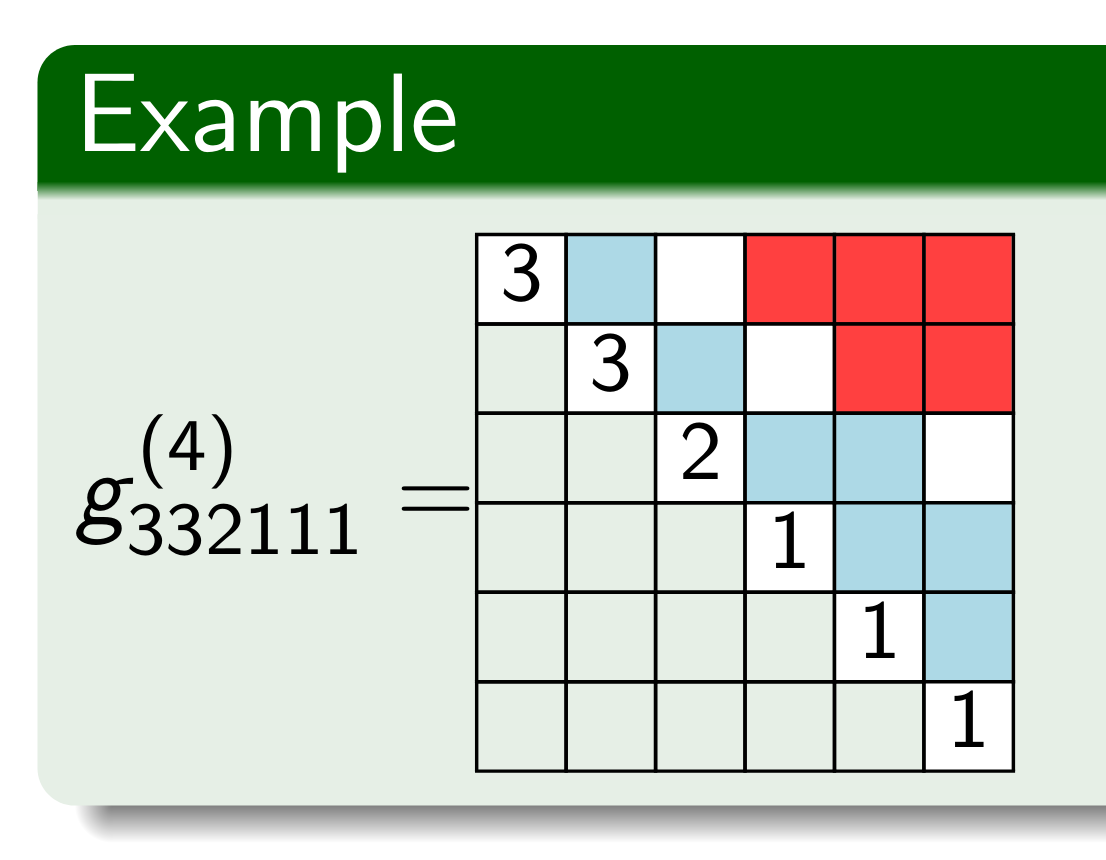
This last weekend, I had an opportunity to attend and present a poster at the 2019 Mid-Atlantic Algebra, Geometry, and Combinatorics (MAAGC) conference in Philadelphia. The poster is about one of the projects I am currently working on to describe “\(K\)-theoretic \(k\)-Schur functions” with a raising operator formula which is a specialization of what we are currently calling “\(K\)-theoretic Catalan functions” since they generalize the description of Catalan functions that Blasiak, Morse, Pun, and Summers used to prove the Schur positivity of \(k\)-Schur functions.